Multi GBDT点击率预估实战:修改XGBoost,并行训练数千个GBDT模型
说明:本文的内容是我在15年末到16年初的相关工作,所写内容纯从技术角度出发,并不涉及具体业务,文中提到的所有东西都来自公开的网页和源码。
FaceBook出来GBDT+LR后,当时很多团队都做了很多相关工作。但多是一个GBDT来transform原始特征。为了更好的利用特征数据,我们尝试了对不同属性的训练样本,训练不同的GBDT模型,用Muti GBDT来transform特征。
为了能得到多个GBDT模型,修改了XGBoost的hadoop streaming,能在yarn平台上支持数千个GBDT的训练。这些模型使用的样本数,从几万,到几千万不等,3个小时以内能全部训练完成。最后将模型推送到线上的点击率预估算法使用。
本文的结构如下:
第一部分:XGBoost训练的GBDT理论介绍。重点是如何一步步的最优化损失函数。
第二部分:如何在yarn平台上并行训练数千个GBDT模型。
第三部分:解释为什么要使用Multi GBDT。
第四部分:模型调优。
1. Boosted tree来做点击率预估的公式推导
首先来定义树模型,假设第i行输入特征为$x_{i}$,第$k$颗树为$f_{k}$,那树模型的输出就可以写成 :
目标损失函数就可以写成如下形式,一个误差函数,加上一个正则化项:
那如何来训练树模型来最小化这个目标函数呢?XGBoost使用方法为additive training,核心思路就是,每次加入一颗树,使得目标函数最小。于是我们的目标函数可以改写成:
将这个式子再通过泰勒展开得到:
其中$g_i=\partial_{\hat{y_i}^{(t-1)}}l(y_i,\hat{y}_i^{(t-1)}),h_i=\partial_{\hat{y_i}^{(t-1)}}^2l(y_i,\hat{y}_i^{(t-1)})$。$g_i$就是指目标值和估计值之间的误差在$\hat{y_i}^{(t-1)}$这个点的一阶导数,$h_i$就是二阶导数。
对于二分类来说,假设点击是1,不点击是0。另x为特征,y为{0,1}。可得:
于是logloss可以写成:
可得$g_i$和$h_i$:
&emsp接下来,对树模型的定义做下细化,将树拆分成结构部分$q$和叶子的权重部分$w$。即$q$就是树节点的那些规则,$w$就是特征通过树规则后得到的叶子节点权值。
目标函数的正则化项可以写成:
定义$I_j={i|q(x_i)=j}$,$I_j$为所有通过树的规则,进入叶子$j$的集合。
再定义$G_j=\sum_{i\in I_j}g_i , H_j=\sum_{i\in I_j}h_i$。我们改写目标函数为:
目标函数一步步推导到这个形式,就会发现,最小化目标函数,其实就是一个二次函数求导的问题。最小化的目标函数值为:
$Obj=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j^2+\lambda}+\gamma T$,其中$w_j=-\frac{G_j}{H_j+\lambda}$
所以,我们每次加入一颗树,就是要想办法将这个目标函数最小化。怎们分裂这个部分我想放到下一篇里面,来讲下如何用GBDT来做特征选择。
2. XGBoost并行训练数千个GBDT模型
XGBoost的源码:https://github.com/dmlc/xgboost。
XGBoost在yarn平台的运行命令是:
但是它无法实现对多份训练数据同时并行训练多个GBDT模型 。
例如:我们有100份训练数据,每份训练数据都希望得到一个GBDT模型,那就需要xgboost同时训练100个模型。
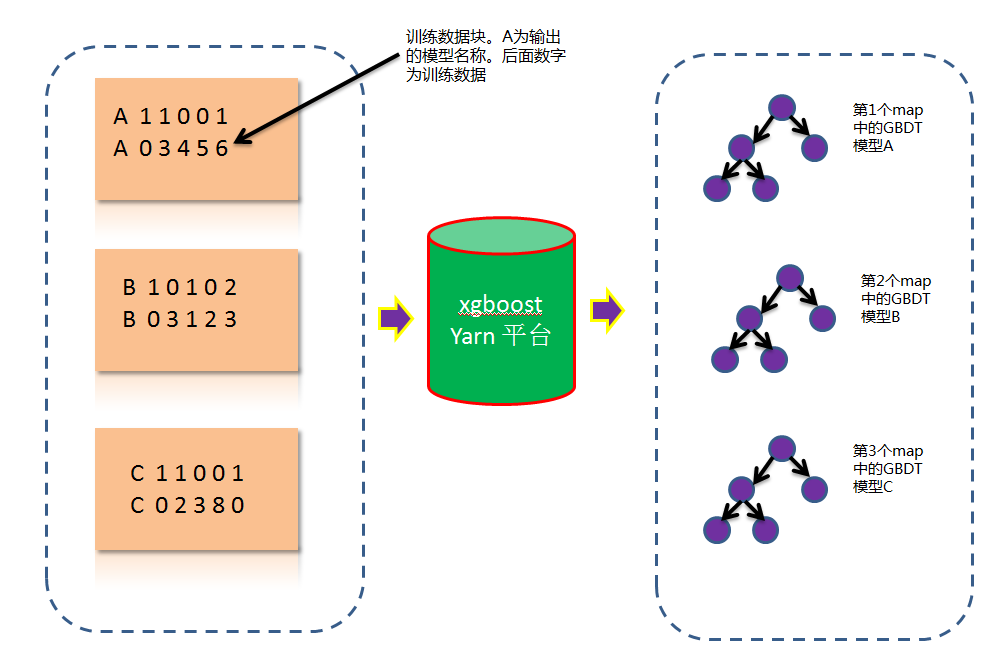
我们修改了hadoop streaming流,在对数据做map的时候,不做shuffle,一个数据块就输入到一个map。在每个map里面都运行一个xgboost。如下图:
其中黑框里面表示输入输出的路径。由于数据量很大,红框里面必须要设置。否者会报错:Java.lang.OutOfMemoryError: Java heap space 。
蓝色框里面是最核心部分,需要额外编译一个java包,来指明数据不需要分块。实现的代码如下:
3. Multi GBDT+X系列 点击率预估
从Facebook发出论文“Practical Lessons from Predicting Clicks on Ads at facebook”开始。就开始出现了GBDT+X点击率预估系列,X可以是LR,FM,DNN。
为了更精细化训练数据的使用,其实可以对训练数据分成不同的种类。
例如:可以通过人群的兴趣爱好来分,有的喜欢体育,有的喜欢金融。细分的化可能有上千种。
这种很稀疏的离散特征,如果在业务场景中又非常重要,只用一个GBDT来表示这堆训练数据,那很有可能训练节点中是无法充分利用好这个特征的。
那其实可以对每种兴趣的训练数据都训练一个GBDT,这样每个模型本身就带有该兴趣的属性了。
最终用来做预估的时候,就变成了Multi GBDT + LR or FM or DNN了
4.模型调优
我觉得xgboost相对于dnn,很大的一个优点就是调优的方向是很明确的,参数就那么几个。DNN可尝试的网络结构太多,反而很容易就迷失。
看下基本的参数: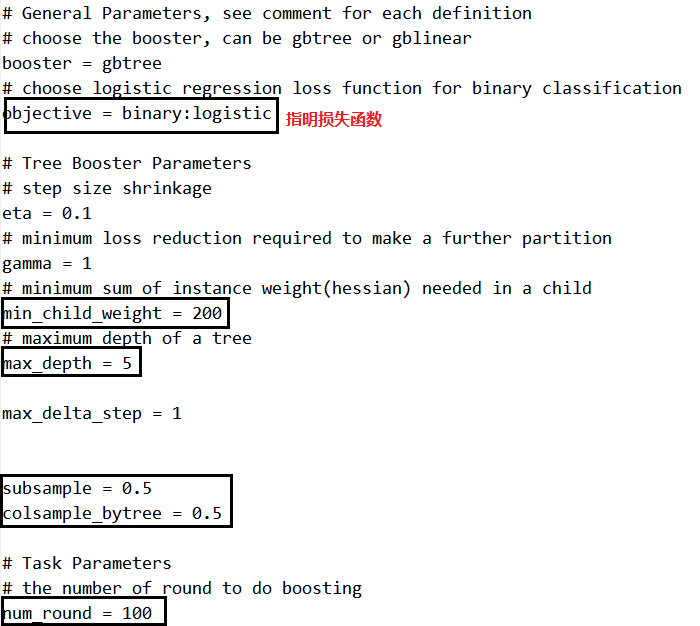
tree ensemble里面最重要就是防止过拟合。
min_child_weight是叶子节点中样本个数乘上二阶导数后的加和,用来控制分裂后叶子节点中的样本个数。样本个数过少,容易过拟合。
subsample是行采样,设置的越小,每棵树之间的使用的样本数就越不相同,数学上有证明,这样模型的variance会越小。
colsample_bytree是列采样,设置的越小,树之间使用的特征差异越大,也是用来降低模型variance的。
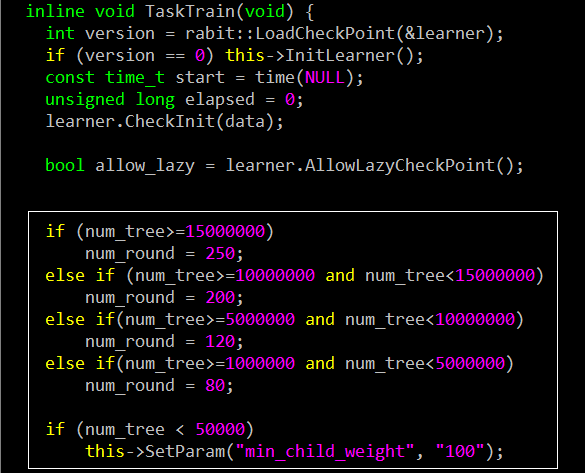
由于我们同时训练上千个模型,所以在XGBoost里面加入了一个逻辑。对不同大小的训练数据,设置不同的树颗数。该段代码在xgboost_main.cpp中。这样做对效果提升挺明显了,如果所有的GBDT模型都设置一样的树颗数,当这个值过大时,会导致很多小训练样本的GBDT模型过拟合。当这个值过小时,又会导致大训练样本的GBDT模型欠拟合。